技术分享 | 坐标测量机不确定度因素-采样策略

“采样策略”解决为了测量一个几何元素，如一个圆，应当怎样合理地选择采样点？这些点的位置应怎样选择的问题。

采样策略

为了测量一个几何元素，如一个圆，应当怎样合理地选择采样点？这些点的位置应怎样选择？这就是采样策略要研究的问题。

所谓合理选择, 是指在相同的条件下即相同的测量机、相同的工件、相同的环境条件下，应怎样安排采样点的位置，以使被测参数有较高的测量精度，耗费的时间也不致太多。

采用不同的采样点数和位置，会引起不同的测量结果。这主要是由于：①被测元素非理想元素，有形状误差；②测量机非理想测量机，有测量误差。这里包括由于环境条件等因素引起的误差。

不同采样策略影响示例1

下图是一个圆形工件，有三叶形误差。若在相隔 120°，三个均布点上进行测量，当测量点选择在a,b,c三点时，测得的直径最小。当测量点选择在A,B,C三点时，测得的直径最大。由于工件安放位置的随机性等，测得的可能是它们之间的任意值。测得的最大直径与最小直径之差是圆度误差的两倍。上述讨论是在测量机没有误差情况下作出的。当测量机有误差时,测得结果差别还可能增大。对于一个理想的圆，当测头具有三叶形误差时(它是测量机误差的一部分),也会产生类似结果。实测的结果反映两者综合影响。

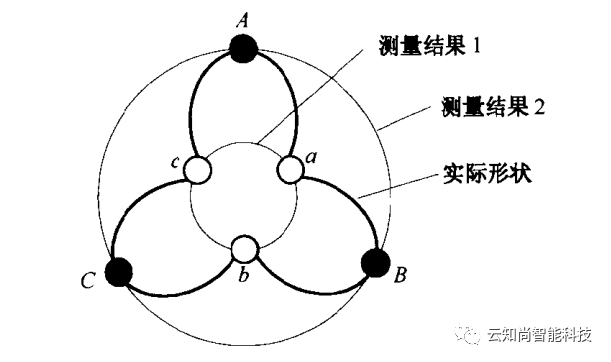
不同采样策略的影响1

不同采样策略影响示例2

工件形状如曲线 2 所示。若采样点选在A,B,C三点，测得的圆直径较小，如图中圆3所示。若采样点选在A',B',C'三个点,则测得的直径很大，如圆1所示。若在A',C'两点测量误差向外，而B'点测量误差向内，这时测得的直径更大，如圆 4 所示。

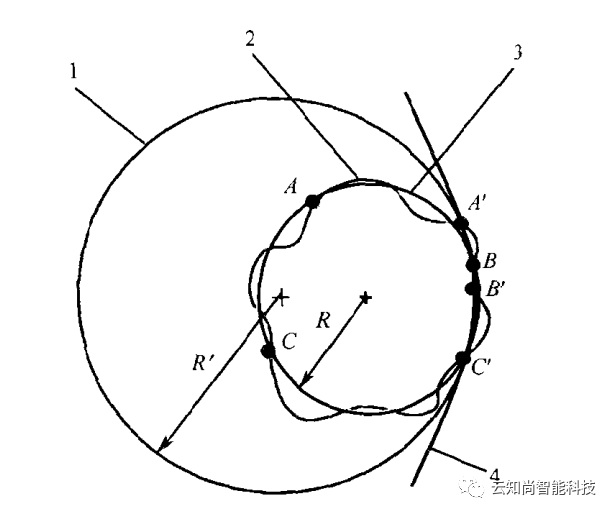
不同采样策略的影响2

从上面的例子中可以看到，采样策略对测量结果有很大影响。不正确的采样，如图8.7-6中A',B',C'三个采样点密集在一起，微小的形状误差或测量误差，会对测量结果带来很大影响,即造成很大的测量不确定度。

分析采样策略质量的方法

分析采样策略的方法也有两种：一种是解析法，另一种是计算机仿真法。

在解析法中，首先列出给定的采样方式下被测参数与采样点坐标之间的关系。在采样点超出最小必需采样点数时，例如通过在4个或4个以上点的采样，测量圆的直径或中心位置，在求被测参数与采样点坐标之间的关系时，常以按最小二乘条件求出的替代元素的参数作测得的被测参数。在计算中假定被测参数有某些形状误差，形状误差常以含有各次谐波误差的形式给出。对于测量误差，常给出范围与分布规律,最常用的分布规律是正态分布。这是因为在对测量机的几何误差作软件补偿后,残余误差主要是随机误差，一些不能确定的系统误差的值也具有随机性。然后,根据这二类误差算出被测参数的测量不确定度。

在计算机仿真法中，首先按照被测工件的形状误差规律将被测元素的函数表达式或点集坐标值存在计算机中，然后按采样方式规定的规律采样。例如在按120°间隔等分采样时,第一采样点的位置是随机的，其它两点相应地与之相隔120°,240°。在需要考虑测量误差时，在这些采得的坐标值基础上再加上测量误差。然后根据这些点的值再确定被测参数值。随着第一采样点的位置变化，并且测量误差的影响具有随机性，计算得到的被测参数值会不同，被测参数的分散性即为被测参数的测量不确定度。